انرژی بستگی هسته

با استفاده از روش‌های طیف‌سنجی جرمی می‌توان جرم اتم‌ها را با دقتی بیش از ${\displaystyle {10}^{-5}}$ واحد اندزه گیری کرد. این اندازه‌گیری‌های دقیق نشان می‌دهند که جرم یک هسته از مجموع جرم‌های نوترون‌ها و پروتون‌های تشکیل‌دهنده‌اش کمتر است. این اختلاف جرم را کاستی جرم می‌نامند. انرژی بستگی هسته همان انرژی معادل کاستی جرم است که هنگام تشکیل هسته آزاد شده‌است.

برای محاسبهٔ انرژی بستگی، جرم هستهٔ ${\displaystyle X}$ را با ${\displaystyle {M}_{x}}$، جرم یک پروتون را با ${\displaystyle {M}_{p}}$، جرم یک نوترون را با ${\displaystyle {M}_{n}}$، تعداد پروتونها را با ${\displaystyle Z}$ و تعداد نوترون‌ها را با ${\displaystyle N}$ نشان می‌دهیم. همان‌طور که گفته شد جرم هسته کمتر از مجموع جرم نوترون‌ها و پروتون‌هایش است، یعنی:

${\displaystyle N{M}_{n}}$ + ${\displaystyle Z{M}_{p}}$ > ${\displaystyle {M}_{x}}$

این کاستی جرم را با ${\displaystyle M}$${\displaystyle \triangle }$ نشان می‌دهیم که برابر است با:

${\displaystyle {M}_{x}}$ - ${\displaystyle Z{M}_{p}}$ + ${\displaystyle N{M}_{n}}$

حال با استفاده از معادلهٔ اینشتین یعنی ${\displaystyle E=M{C}^{2}}$ انرژی معادل آن را حساب کنیم:

${\displaystyle {E}_{b}}$ = ${\displaystyle \triangle }$${\displaystyle M}$${\displaystyle {C}^{2}}$ = [${\displaystyle Z{M}_{p}}$ + ${\displaystyle N{M}_{n}}$-${\displaystyle {M}_{x}}$]${\displaystyle C}$²

انرژی بستگی را با علامت ${\displaystyle {E}_{b}}$ نشان می‌دهند.

معادله فوق مقدار انرژی بستگی هستهٔ ${\displaystyle X}$ را به دست می‌دهد که با توجه به بزرگی مقدار سرعت نور (${\displaystyle C}$)، انرژی محاسبه شده مقدار بسیار بزرگی خواهد بود. به همین دلیل در واکنش‌های هسته‌ای هرچند در مقیاس‌های کوچک، انرژی بسیار زیادی مبادله می‌شود.

با استفاده از انرژی بستگی می‌توان انرژی تولید شده در واکنش‌هایی مانند همجوشی هسته‌ای یا شکافت هسته‌ای را محاسبه کرد.[2]

برای محاسبهٔ انرژی بستگی هسته بر حسب عدد جرمی (A) و عدد اتمی (Z)، فیزیکدان آلمانی کارل فردریک فون وایتساکر رابطه زیر را در سال ۱۹۳۵ ارائه کرد. این رابطه به «فرمول وایتساکِر» و یا «فرمول نیمه تجربی جرم» معروف است.

${\displaystyle E_{B}=a_{1}A-a_{2}A^{2/3}-a_{3}{\frac {Z(Z-1)}{A^{1/3}}}-a_{4}{\frac {(A-2Z)^{2}}{A}}+\delta (A,Z)}$

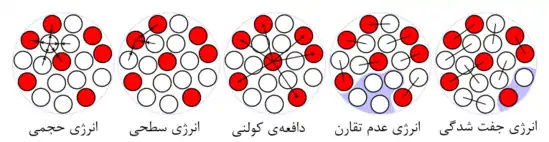
فرمول نیمه‌تجربی جرم بر اساس مدل قطره مایعی هسته به دست آمده است. این مدل، هستهٔ اتم را به صورت قطرهٔ مایعی در نظر می‌گیرد که نوترون‌ها و پروتون‌ها نقش مولکول‌هایش را دارند. با در نظر گرفتن این مدل، برای محاسبهٔ انرژی بستگی هسته نقش پنج انرژی را باید در نظر گرفت که به ترتیب در پنج جملهٔ فرمول لحاظ شده‌اند:

1. جمله اول مربوط به انرژی ربایشی بین نوکلئون‌های مجاور یکدیگر است (انرژی حجمی)
2. جمله دوم مربوط به نوکلئون‌هایی است که در سطح هسته قرار دارند. این‌ها فقط با نوکلئون‌های درونی برهم‌کنش دارند و در نتیجه انرژی بستگی آن‌ها نسبت به نوکلئون‌های داخلی کمتر است (انرژی سطحی).
3. جمله سوم مربوط به انرژی دافعهٔ کولنی بین پروتون‌ها است که باعث تضعیف انرژی بستگی کل می‌شود (انرژی دافعه کولنی).
4. جمله چهارم مربوط به عدم تقارن تعداد نوکلئون‌ها است. چرا که در هسته‌هایی که N نوترون و Z پروتون دارند، حداکثر انرژی بستگی زمانی حاصل می‌شود که تعداد نوترون‌ها و پروتون‌ها با هم برابر باشد N=Z. در غیر اینصورت هسته انرژی بستگی کمتری خواهد داشت (انرژی عدم تقارن).
5. جمله پنجم نیز مربوط به جفت شدگی نوکلئون‌ها در هسته است که در نوکلئون‌هایی که تعداد نوترون‌ها و پروتون‌ها زوج-زوج است باعث افزایش و در نوکلئون‌های فرد-فرد باعث کاهش انرژی بستگی می‌شود. برای هسته‌های با عدد جرمی فرد انرژی جفت شدگی صفر است (انرژی جفت شدگی).

در فرمول مذکور، داده‌های زیر به صورت تجربی به دست آمده‌اند:

تأثیر عوامل مختلف بر انرژی بستگی هسته در مدل قطره مایعی

${\displaystyle 15.56MeV}$=${\displaystyle a_{1}}$

${\displaystyle 17.23MeV}$=${\displaystyle a_{2}}$

${\displaystyle 0.697MeV}$=${\displaystyle a_{3}}$

${\displaystyle 23.28MeV}$=${\displaystyle a_{4}}$

${\displaystyle \pm 11.18 \over A^{1/2}}$ =${\displaystyle \delta (A,Z)}$ که در حالت زوج-زوج مثبت، در حالت فرد-فرد منفی و در حالت فرد بودن عدد جرمی، برابر صفر است.

با استفاده از این مقادیر، فرمول وایتساکر تطابق نسبتاً قابل قبولی با نتایج تجربی نشان می‌دهد.[3]

در واکنش‌های هسته‌ای جرم و انرژی به یکدیگر تبدیل می‌شوند. از آن‌جا که مقدار جرم مبادله شده بسیار کوچک است، معمولاً از واحد جرم اتمی استفاده می‌شود که با u نمایش داده می‌شود. ۱u معادل ${\displaystyle {\frac {1}{12}}}$ جرم ایزوتوپ کربن-۱۲ است که طبق تعریف برابر ۱۲/۰۰۰۰۰۰u می‌باشد. برای انرژی بستگی نیز از واحد الکترون‌ولت استفاده می‌شود. با استفاده از معادلهٔ ${\displaystyle E=M{C}^{2}}$ می‌توان جرم و انرژی را بر حسب این دو واحد به همدیگر تبدیل کرد:[2]

۱u =۹۳۱/۵ × ۱۰^۱۹ eV

منحنی اَستون: نمودار انرژی بستگی متوسط بر حسب عدد جرمی

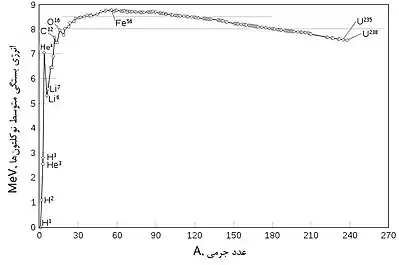
اگر مقدار انرژی بستگی را بر تعداد نوکلئون‌های تشکیل دهندهٔ یک هسته تقسیم کنیم، "انرژی بستگی متوسط هر نوکلئون" به دست می‌آید. از رسم این کمیّت بر حسب عدد جرمی، نموداری برای انرژی بستگی متوسط به دست می‌آید که به افتخار فرانسیس ویلیام اَستون فیزیک‌دان انگلیسی، "منحنی استون" نامیده می‌شود.[1] مطالعهٔ این نمودار اطلاعات مفیدی دربارهٔ نیروی هسته‌ای قوی و پایداری هسته‌های مختلف به دست می‌دهد:

• کاشیگر، لطیف (۱۳۹۴). فرهنگ فیزیک. ۳. تهران: فرهنگ معاصر. شابک ۹۷۸-۶۰۰-۱۰۵-۱۰۳-۶.
• شورای مؤلفان (۱۳۹۴). فیزیک پیش‌دانشگاهی. رشتهٔ علوم ریاضی. تهران: شرکت چاپ و نشر کتاب‌های درسی ایران. شابک ۹۶۴-۰۵-۱۱۵۷-۹.
• ریگدن، جان و دیگران (۱۳۸۱). دانشنامه فیزیک. ۱. ترجمهٔ محمد ابراهیم ابوکاظمی و دیگران. زنجان: مکان مرکز تحصیلات تکمیلی در علوم پایه. شابک ۹۶۴-۵۵۱۵-۳۵-۱.
• می‌یرهوف، والتر (۱۳۷۱). مبانی فیزیک هسته‌ای. ترجمهٔ محمد فرهاد رحیمی. مشهد: مؤسسهٔ چاپ و انتشارات دانشگاه فردوسی مشهد.
• لییزر، کارل هاینریش (۱۳۸۲). شیمی هسته ای و رادیوشیمی؛ مبانی و کاربردها. تهران: سازمان انرژی اتمی ایران. شابک ۹۶۴-۸۲۳۴-۰۷-۸.