اتوماتون تعیین‌ناپذیر متناهی

در تئوری محاسبات، اتوماتون تعیین‌ناپذیر متناهی یا اتوماتون غیرقابل تعیین متناهی یا یا ان‌اف‌اِی (Nondeterministic finite automaton - NFA) به اوتوماتون‌هایی گفته می‌شود که در مورد آن‌ها برای برخی از دوتایی‌های حالت و سمبل ورودی امکان عبور به بیشتر از یک حالت جدید اجازه داده شده باشد.
NFA در بعضی موارد با نام Subshift of finite type شناخته می‌شود.NFA به راه‌های متعددی , تعمیم داده شده‌است:اتومات تعین ناپذیر با ε حرکت[1] , اتوماتون پشته‌ای ,اتومات ω ای[2]،اتومات احتمالی[3].

تعریف غیررسمی

یک NFA , مانند DFA به رشته‌ای از نمادها برای ورود نیازمند است. برای هر نماد ورودی، NFA به حالتی جدیدی میرود تا بتواند تمام ورودی جدید را استفاده کند. برخلاف NFA ,DFA غیر قطعی است و برای هر نماد ورودی , حالتی بعدی می‌تواند هر کدام از چندین حالت ممکن باشد , بنابراین در تعریف رسمی حالت بعدی عضوی از مجموعه توانی از وضیعت هاست که در یک زمان در نظر گرفته می‌شود. مفهوم پذیرفتن یک ورودی در NFA به مانند DFA است. DFA زمانی پذیرفته می‌شود اگر و تنها اگر که آخرین نماد ورودی استفاده شده ِهنوز تعدادی انتقال باشد که به حالت مورد انتظار و مورد قبول برسیم. معادلاَ زمانی به رد می‌شود که بدون توجه به آنچه انتقال پیدا کرده‌است , به حالت مورد قبول نرسیم.

تعریف رسمی

یک NFA به‌طور معمول با ۵ عامل معرفی می‌کنیم:(Q, Σ, Δ, q0, F) که در آن:

  • Q مجموعه محدودی از وضیعت هاست.
  • Σ مجموعه محدودی از وضیعت‌های ورودی است.
  • ( Δ : Q × Σ → P(Q رابطه انتقال است.
  • q0 ∈ Q حالت اولیه است.
  • F ⊆ Q مجموعه از حالت مورد قبول است.

حال توجه کنید که منظور از (P(Q مجموعه توانی از Q است. فرض کنید که w = a1a2 ... an مجموعه ورودی باشد(Σ). اتومات به شرطی دنباله w را میپذیرد که شرایط زیر را داشته باشد:

  1. r0 = q0
  2. ri+1 ∈ Δ(ri, ai+1), for i = 0, ..., n−1
  3. rn ∈ F.

به عبارت دیگر , شرط اول می‌گوید که ماشین با q0 شروع به کار می‌کند.شرط دوم می‌گوید که ماشین هر کاراکتر رشته w را از حالت خود به حالت تابع Δ انتقال می‌دهد. و شرط سوم می‌گوید که ماشین زمانی w میپذیرد که آخرین ورودی w در یکی از حالات مورد قبول ماشین باعث توقف شود. در غیر اینصورت اتومات رشته ورودی را رد می‌کند. مجموعه‌ای از رشته‌هایی که پذیرفته می‌شوند را با زبان صوری M نشان میدهیم و برای نشان دادن این زبان از(L(M استفاده می‌کنیم.

همچنین می‌توان(L(M را با ( Δ*: Q × Σ* → P(Q تعریف کرد بدین صورت که:

  1. 1- ( Δ*(r, ε)= {r در جاییکه ε رشته‌ای خالی است.
  2. 2- If x ∈ Σ*, a ∈ Σ

و <Δ*(r, x)={r1, r2,..., rk

Δ*(r, xa)= Δ(r1, a)∪...∪Δ(rk,a):THEN

در نتیجه: {L(M) = {w | Δ*(q0, w) ∩ F ≠ ∅.

توجه کنید که داشتن یک حالت اولیه منفرد لازم نیست. در برخی موارد NFAها دارای چند حالت اولیه‌اند. یک ساختار اتومات وجود دارد که چند حالت اولیه را به یک حالت اولیه تبدیل می‌کند.
یرای آگاهی بیشتر از تعریف رسمی می‌توانید صفحه نظریه اتوماتا را ببینید.

مثال

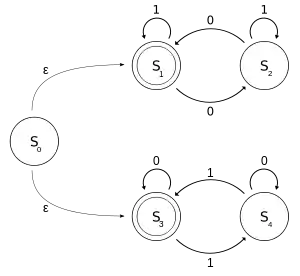
در این مثال یک ماشین ان‌اف‌ای با الفبای دوتایی شرح داده شده‌است. این ماشین تشخیص می‌دهد که آیا یک رشته ورودی تعدادی زوج صفر در بر دارد یا تعدادی زوج یک.

اتوماتون M را به صورت در نظر می‌گیریم:

M = (Q, Σ, T, s0, F)

  • Σ = {0, 1},
  • Q = {s0, s1, s2, s3, s4},
  • E({s0}) = { s0, s1, s3 }
  • F = {s1, s3}, and
  • The transition function T can be defined by this state transition table:
0
1
ε
S0
{}
{}
{S1, S3}
S1
{S2}
{S1}
{}
S2
{S1}
{S2}
{}
S3
{S3}
{S4}
{}
S4
{S4}
{S3}
{}

انواع NFA

ماشین‌های تعین‌پذیر حالات متناهی DFA : به آن‌دسته از ماشین‌های حالات متناهی اطلاق می‌شود که در آن‌ها به ازاء هر دوتائی[4] شامل حالت[5] و ورودی یک و فقط یک امکان برای عبور به حالت بعدی وجود داشته باشد.

ماشین تعیین ناپذیر با ε حرکت[1]:این اتومات‌ها می‌توانند رابطه انتقال را تغییر دهند و به این شکل دربیاورند:(Δ : Q × (Σ ∪{ε}) → P(Q

شباهت با DFA

به ازای هر DFA , NFA وجود دارد که دارای زبان صوری یکسان‌اند.DFA را می‌توان به کمک ساختمان پاورست ساخت. و همچنین مهم است که بتوان ساختارهای NFAها را به ساختار DFAهایی با کیفیت تر تبدیل کرد. البته ممکن است که اگر یک NFA دارای n وضیعت باشد آنگاه ساختار DFA دارای ۲n وضیعت باشد که این عدد نمادی در بعضی موارد در مقادیر بزرگ می‌تواند مشکل ساز باشد.

خواص و ویژگی‌ها

ماشین با یک وضیعت اولیه کار خودش شروع می‌کند و رشته‌ای از نمادها را دریافت می‌کند. اتوماتا حالت اولیه را توسط ماشین‌های حالات متناهی Δ به حالت جدید تبدیل می‌کنند. توجه کنیم که وضیعت NFA تنها به حالت حاضر بستگی ندارد بلکه به ورودی‌های بعدی نیز ریط دارد. تا زمانی که تمام ورودی‌های بعدی اتفاق نیفتند غیرممکن است که وضیعت ماشین را متوجه شویم.[6] زمانی که NFA دریافت ورودی را تمام کرد آنگاه درمرحله پذیرش است و اعلام می‌کند رشته پذیرفته شدهاست در غیر این صورت رشته را رد می‌کند.

به رشته‌هایی که NFA آن را میپذیرند یک زبان مورد پذیرش NFA گویند. این زبان ,زبان منظم است.

اجرا

راه‌های بسیاری برای اجرا NFA وجود دارد که برخی از آن‌ها عبارتند از :

۱- آن را به DFA معادل تبدیل می‌کنیم. در برخی موارد این کار سبب افزایش تصاعدی حجم ماشین و بنابراین به وجود آمدن فضاهای کمکی متناسب با تعداد حالت‌های NFA می‌شود(برای نگهداری مقدار حالت برای هر حالت در NFA حداکٹر به یک بیت حافظه نیاز است)[7]

۲-یک ساختمان داده برای تمام حالاتی که ماشین ممکن است در حال حاضر در آن باشد نگهداری کنیم. در مصرف آخرین ورودی که ماشین می‌گیرد، اگر یکی از این حالت‌ها حالت نهایی باشد آن رشته را ماشین می پذیرد. اگر برای هر حالت NFA یک بیت هزینه شود همانند روش قبلی در بدترین حالت زمان گرفته می‌شود.[8]

کارایی NFA

DFA و NFA از این نظر به هم شباهت دارند که اگر NFA توسط زبانی شناخته شوند , DFA نیز توسط آن زبان شناخته می‌شود. که توجه به این خاصیت مهم و مفید است. مفید است زیرا ساختن یک NFA از یک زبان راحت‌تر از ساختن DFA از آن زبان است. و از این نظر اهمیت دارد که NFA می‌تواند پیچیدگی بسیار از مسائل را که درنظریه محاسبات را کاهش دهد. به‌طور مثال اثبات closure properties از زبان منظم به وسیله NFA ساده‌تر از DFA است.

منابع
  1. Nondeterministic finite automaton with ε-moves
  2. ω-automaton
  3. Probabilistic automaton
  4. Pair
  5. State
  6. Finite State Machine
  7. http://cseweb.ucsd.edu/~ccalabro/essays/fsa.pdf
  8. http://en.wikipedia.org/wiki/Nondeterministic_finite_automaton
  • Sudkamp, T. A., An Introduction to the Theory of Computer Science, Languages and Machines, 3rd ed., Pearson Education, Inc., 2006. ISBN 0-321-32221-5
  • M. O. Rabin and D. Scott, "Finite Automata and their Decision Problems", IBM Journal of Research and Development, 3:2 (1959) pp. 115–125.
  • Michael Sipser, Introduction to the Theory of Computation. PWS, Boston. 1997. ISBN 0-534-94728-X. (see section 1.2: Nondeterminism, pp.47–63.)
  • John E. Hopcroft and Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley Publishing, Reading Massachusetts, 1979. ISBN 0-201-02988-X. (See chapter 2.)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.