ساختمان پاورست
در نظریه محاسبات ونظریه اتوماتا , ساختمان پاورست یا زیر مجموعه ساختمان یکی از روشهای تبدیل کردن یک اتوماتون تعینناپذیر متناهی (NFA) به ماشینهای تعینپذیر حالات متناهی (DFA) میباشد که شبیه تشخیص زبان صوری میباشد. در این نظریه خیلی مهم است زیرا که براساس NFA بناشدهاست اگر چه انعطافپذیری زیادی دارد ولی قادر به شناسایی تمام زبانهایی که توسط DFA شناسایی میشود نیست. به بیان دیگر NFA انعطافپذیری زیادی دارد اما چون بعضی از زبان ها را قادر به تبدیل به DFA نیستند را نمیتوان به صورت فرمولی در آورد بخاطر همین کاراییش کمتر از DFA هست حتماً باید تبدیل شود تا بتوان گفت فرمولی برایش وجود دارد.
این خیلی مهم است برای تمرین تبدیل کردن ساختار آسانتر NFA به DFA بسیار کارآمد انجام پذیرد در حالی که اگر , n ایستگاه دارد , نتیجه تبدیل به DFA میتواند 2n ایستگاه داشته باشد , یک عدد بزرگ نمایی که بعضی از اوقات ساختار غیر عملی برای NFAهای بزرگ میشود(نمیشود تبدیل کرد).
این ساختار , بعضی اوقات Rabin–Scott powerset construction یا زیر مجموعهٔ ساختار نامیده میشود. تا با این واسطهٔ متمایزی بین ساختارهای متشابه برای نوعهای دیگر از اتوماتون قائل شونند که اولین بار توسط مایکل رابین و دانا اسکات در 1995 بیان شد.
ساختار
ساختمان پاورست بهطور مستقیم به NFA اعمال میشود بطوریکه تغییرات حالت، بدون مصرف نمادهای ورودی (با نام " ε-moves ") اجازه نمیدهد. چنین ماشینی میتواند به عنوان 5-عنصر (Q, Σ, T, q0, F) در نظر گرفته شود که در آن Q مجموعهای از حالات تعریف شدهاست، Σ مجموعهای از نمادهای ورودی، T تابع انتقال (که یک حالت و نماد ورودی را به یک مجموعه از حالتها می نگارد، q0 حالت اولیه است و F مجموعهای از حالات پذیرش است. DFA مربوطه، حالاتی که زیر مجموعه Q میباشد را داراست . حالت اولیه برای ماشینهای تعینپذیر حالات متناهی , {q0} میباشد که مجموعهای تک عضوی از حالات اولیه است. تابع انتقال DFA حالت S را (به نمایندگی از یک زیر مجموعه از Q ) وسمبل ورودی X را به مجموعه { T(S,x) = ∪{T(q,x) | q ∈ S می نگارد، مجموعهای از همه حالات که میتواند با گذارX از حالت در S تحقق یابد. حالتS از DFA حالت پذیرا است اگر و تنها اگر حداقل یک عضو S یک حالت پذیرا از NFAباشد.
مثال
NFA زیر دارای 4 حالت است. حالت 1 , حالت اولیه است و حالت 3 و 4 حالت پذیرفته شدهاست. الفبای آن شامل 2 نماد 0 و1 است. و دارای ε-moves است. حالت 1 , حالت اولیه است.
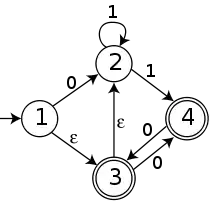
حالت اولیه DFA ساخته شده از NFA مجموعهای از تمام حالتهایی از NFA است که میتوانند از حالت 1 با ε حرکت قابل رسیدن است. انتقال از {1,2,3} با نماد ورودی 0 با پیکانی از حالت 1 به حالت 2 ادامه میدهد. و همچنین نه حالت 2 و حالت 4 خروجی ε-moves دارند. در نتیجه{T({1,2,3},0) = {2,4 و و با همان استدلال DFA کامل ساخته شده از NFA در زیر نشان داده شدهاست.
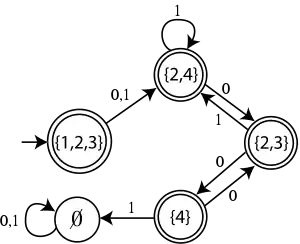
جستارهای وابسته
منابع
- Michael Sipser, Introduction to the Theory of Computation ISBN 0-534-94728-X. (See . Theorem 1.19, section 1.2, pg. 55.)
- John E. Hopcroft and Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley Publishing, Reading Massachusetts, 1979. ISBN 0-201-02988-X. (See chapter 2.)
- James Andrew Anderson; Thomas J. Head (2006). Automata theory with modern applications. Cambridge University Press. pp. 43–49. ISBN 978-0-521-84887-9.
- Klaus Schneider (2004). Verification of reactive systems: formal methods and algorithms. Springer. pp. 210–212. ISBN 978-3-540-00296-3.
- M. O. Rabin and D. Scott. Finite automata and their decision problems. IBM Journal of Research and Development, 3(2):114–125, 1959